View on QuantumAI View on QuantumAI
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
|
This notebook demonstrates how to use a Quantum Virtual Machine with larger, more elaborate circuits to demonstrate stabilizer circuits and how they can reveal hardware errors.
Install Cirq and qsim, Create Quantum Virtual Machine
# @title Install `cirq_google` and `qsimcirq`
try:
import cirq
import cirq_google
except ImportError:
print("installing cirq...")
!pip install --quiet cirq-google
print("installed cirq.")
import cirq
import cirq_google
try:
import qsimcirq
except ImportError:
print("installing qsimcirq...")
!pip install --quiet qsimcirq
print(f"installed qsimcirq.")
import qsimcirq
# Other modules used in this colab
import matplotlib.pyplot as plt
import time
import random
# @title Create Quantum Virtual Machine: Choose a processor ("willow_pink", "rainbow" or "weber")
# (see cirq_google.engine.list_virtual_processors() for available names)
processor_id = "willow_pink" # @param {type:"string"}
# Instantiate the engine.
sim_engine = cirq_google.engine.create_default_noisy_quantum_virtual_machine(
processor_id=processor_id, simulator_class=qsimcirq.QSimSimulator
)
print(
"Your quantum virtual machine",
processor_id,
"is ready, here is the qubit grid:",
"\n========================\n",
)
print(sim_engine.get_processor(processor_id).get_device())
Your quantum virtual machine willow_pink is ready, here is the qubit grid:
========================
(0, 6)────(0, 7)────(0, 8)
│ │ │
│ │ │
(1, 5)────(1, 6)────(1, 7)────(1, 8)
│ │ │ │
│ │ │ │
(2, 4)────(2, 5)────(2, 6)────(2, 7)────(2, 8)────(2, 9)────(2, 10)
│ │ │ │ │ │ │
│ │ │ │ │ │ │
(3, 3)───(3, 4)────(3, 5)────(3, 6)────(3, 7)────(3, 8)────(3, 9)────(3, 10)
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │
(4, 2)───(4, 3)───(4, 4)────(4, 5)────(4, 6)────(4, 7)────(4, 8)────(4, 9)────(4, 10)────(4, 11)───(4, 12)
│ │ │ │ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │ │ │ │
(5, 1)───(5, 2)───(5, 3)───(5, 4)────(5, 5)────(5, 6)────(5, 7)────(5, 8)────(5, 9)────(5, 10)────(5, 11)───(5, 12)
│ │ │ │ │ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │ │ │ │ │
(6, 0)───(6, 1)───(6, 2)───(6, 3)───(6, 4)────(6, 5)────(6, 6)────(6, 7)────(6, 8)────(6, 9)────(6, 10)────(6, 11)───(6, 12)───(6, 13)───(6, 14)
│ │ │ │ │ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │ │ │ │ │
(7, 2)───(7, 3)───(7, 4)────(7, 5)────(7, 6)────(7, 7)────(7, 8)────(7, 9)────(7, 10)────(7, 11)───(7, 12)───(7, 13)
│ │ │ │ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │ │ │ │
(8, 2)───(8, 3)───(8, 4)────(8, 5)────(8, 6)────(8, 7)────(8, 8)────(8, 9)────(8, 10)────(8, 11)───(8, 12)
│ │ │ │ │ │ │ │
│ │ │ │ │ │ │ │
(9, 4)────(9, 5)────(9, 6)────(9, 7)────(9, 8)────(9, 9)────(9, 10)────(9, 11)
│ │ │ │ │ │ │
│ │ │ │ │ │ │
(10, 4)───(10, 5)───(10, 6)───(10, 7)───(10, 8)───(10, 9)───(10, 10)
│ │ │ │
│ │ │ │
(11, 6)───(11, 7)───(11, 8)───(11, 9)
│ │ │
│ │ │
(12, 6)───(12, 7)───(12, 8)
Introduction to stabilizer measurements
The following code blocks measure a Z stabilizer as described by Fowler et al (2012). This type of circuit is central to the field of quantum error correction via the idea of a Stabilizer Code.
This circuit is constructed such that the central "measure" qubit will be in the \(|1\rangle\) state if an odd number of the four surrounding "data" qubits (named a-d in the figure) have a bit-flip error (corresponding to an X gate).
Stabilizer measurements on a small grid
The examples below demonstrate a single Z stabilizer, similar to the image above.
Without noise
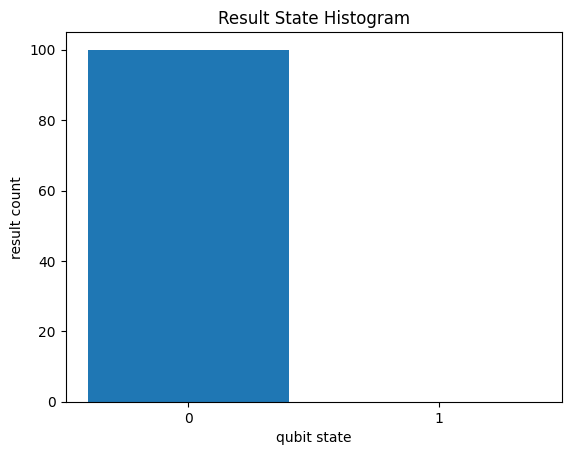
In a perfectly noiseless Z stabilizer, all qubits will remain in the \(|0\rangle\) state.
data_qubits = [cirq.NamedQubit('data_' + str(x)) for x in 'abcd']
measure_qubit = cirq.NamedQubit('_meas')
stabilizer_circuit = cirq.Circuit(
*[cirq.CX(data_qubit, measure_qubit) for data_qubit in data_qubits],
cirq.measure(measure_qubit, key='meas'),
)
print(f'Z-stabilizer circuit:')
print('========================')
print(stabilizer_circuit)
Z-stabilizer circuit:
========================
_meas: ────X───X───X───X───M('meas')───
│ │ │ │
data_a: ───@───┼───┼───┼───────────────
│ │ │
data_b: ───────@───┼───┼───────────────
│ │
data_c: ───────────@───┼───────────────
│
data_d: ───────────────@───────────────
simulator = cirq.Simulator()
result = simulator.run(stabilizer_circuit, repetitions=100)
cirq.plot_state_histogram(result)
<Axes: title={'center': 'Result State Histogram'}, xlabel='qubit state', ylabel='result count'>
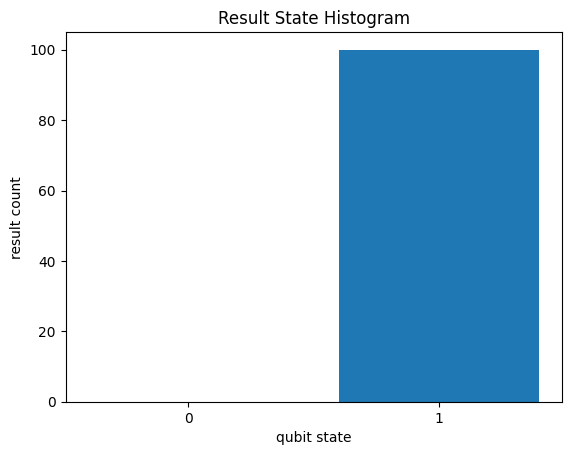
With fixed noise
If one of the qubits is flipped, the measure qubit will also flip to match the parity of the data qubits.
random_data_qubit = random.choice(data_qubits)
stabilizer_circuit_with_error = cirq.X(random_data_qubit) + stabilizer_circuit
print(f'Z-stabilizer circuit with single error:')
print('========================')
print(stabilizer_circuit_with_error)
Z-stabilizer circuit with single error:
========================
_meas: ────────X───X───X───X───M('meas')───
│ │ │ │
data_a: ───────@───┼───┼───┼───────────────
│ │ │
data_b: ───────────@───┼───┼───────────────
│ │
data_c: ───────────────@───┼───────────────
│
data_d: ───X───────────────@───────────────
result = simulator.run(stabilizer_circuit_with_error, repetitions=100)
cirq.plot_state_histogram(result)
<Axes: title={'center': 'Result State Histogram'}, xlabel='qubit state', ylabel='result count'>
With hardware noise on the QVM
With hardware-like noise, the stabilizer circuit becomes much more interesting. An arbitrary error could occur at any point:
- On a data qubit before or after the CNOT
- On the measure qubit before or after the CNOTs
- On the measure qubit between CNOTs
- Multiple errors in any combination of the above locations
The only indication of that error comes from the output of the measure qubit. By creating a grid of stabilizers and observing how they change over time, it's possible to decode when and where errors occured and compensate for them.
The example below only runs a single cycle of one Z stabilizer, so it can't pinpoint error precisely. However, by measuring the data qubits afterwards it's possible to guess at where the error(s) took place.
# Add measurements to the data qubits.
stabilizer_circuit_for_hardware = stabilizer_circuit + (
cirq.Moment(cirq.measure(data_qubit, key=str(data_qubit)[-1]) for data_qubit in data_qubits)
)
print(f'Z-stabilizer circuit with data measurement:')
print('========================')
print(stabilizer_circuit_for_hardware)
Z-stabilizer circuit with data measurement:
========================
_meas: ────X───X───X───X───M('meas')────────────
│ │ │ │
data_a: ───@───┼───┼───┼───────────────M('a')───
│ │ │
data_b: ───────@───┼───┼───────────────M('b')───
│ │
data_c: ───────────@───┼───────────────M('c')───
│
data_d: ───────────────@───────────────M('d')───
# Device_stabilizer_plaquette is an X-shaped region of qubits
# on the actual device.
device_stabilizer_plaquette = [
cirq.GridQubit(5, 3),
cirq.GridQubit(5, 2),
cirq.GridQubit(4, 3),
cirq.GridQubit(5, 4),
cirq.GridQubit(6, 3),
]
if processor_id == "willow_pink":
target_gateset = cirq.CZTargetGateset()
else:
target_gateset = cirq.SqrtIswapTargetGateset()
# Translate the circuit to a suitable gate set.
test_stabilizer_circuit = cirq.optimize_for_target_gateset(
stabilizer_circuit_for_hardware,
context=cirq.TransformerContext(deep=True),
gateset=target_gateset,
)
# Map circuit qubits to hardware ones.
qubit_map = dict(zip([measure_qubit] + data_qubits, device_stabilizer_plaquette))
# Re-map the circuit to the hardware qubits.
test_stabilizer_circuit = test_stabilizer_circuit.transform_qubits(lambda q: qubit_map[q])
print(f'Z-stabilizer circuit optimized for {processor_id}:')
print('========================')
print(test_stabilizer_circuit)
Z-stabilizer circuit optimized for willow_pink:
========================
(4, 3): ───────────────────────────────────────────────────@───PhXZ(a=0,x=0,z=1)────────────────────────────────────────────────────────────────────────────M('b')───
│
(5, 2): ───────────────────────────@───PhXZ(a=0,x=0,z=1)───┼────────────────────────────────────────────────────────────────────────────────────────────────M('a')───
│ │
(5, 3): ───PhXZ(a=0.5,x=0.5,z=0)───@───────────────────────@───────────────────────@───────────────────────@───PhXZ(a=-0.5,x=0.5,z=-8.88e-16)───M('meas')────────────
│ │
(5, 4): ───────────────────────────────────────────────────────────────────────────@───PhXZ(a=0,x=0,z=1)───┼────────────────────────────────────────────────M('c')───
│
(6, 3): ───────────────────────────────────────────────────────────────────────────────────────────────────@───PhXZ(a=0,x=0,z=1)────────────────────────────M('d')───
# Run for 1k repetitions.
repetitions = 1000
start = time.time()
results = sim_engine.get_sampler(processor_id).run(test_stabilizer_circuit, repetitions=repetitions)
elapsed = time.time() - start
print(f'{repetitions} repetitions completed in {elapsed:.03f}s')
1000 repetitions completed in 0.269s
Each result in the histogram below corresponds to a different set of possible errors. Below are some of the most likely cases for each measured result, or "syndrome", but there are many other possible cases not listed.
- No flips (
0_0000) could be no error, or two errors on the same qubit. - A single data flip (e.g.
0_1000) could be a post-CNOT data error, or a pre-CNOT data error and a measurement error. - A data flip and a measure flip (e.g.
1_1000) could be a pre-CNOT data error or post-CNOT errors on both flipped qubits. - Two data flips (e.g.
0_1100) could be pre-CNOT or post-CNOT errors on both flipped qubits.
...and so on, for more unusual cases.
# A labeling function.
def fold_func(bits) -> str:
suffix = "".join(map(str, [bits[i][0] for i in range(1, 5)]))
return f"{bits[0][0]}_{suffix}"
hist = results.multi_measurement_histogram(keys=['meas'] + list('abcd'), fold_func=fold_func)
print("Results (<meas>_<data>)")
ax = cirq.plot_state_histogram(hist)
plt.setp(ax.get_xticklabels(), rotation=30, horizontalalignment='right');
Results (<meas>_<data>)
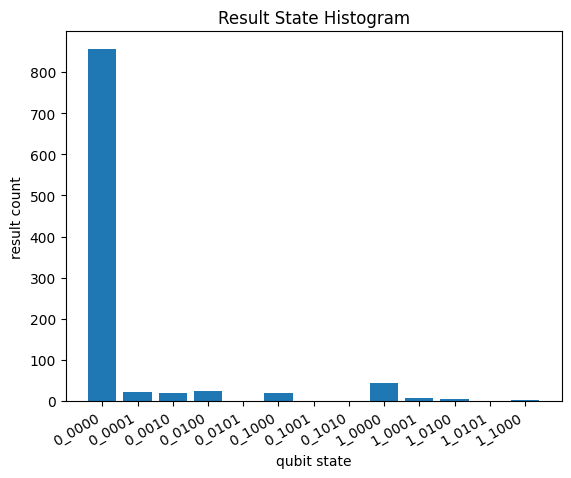
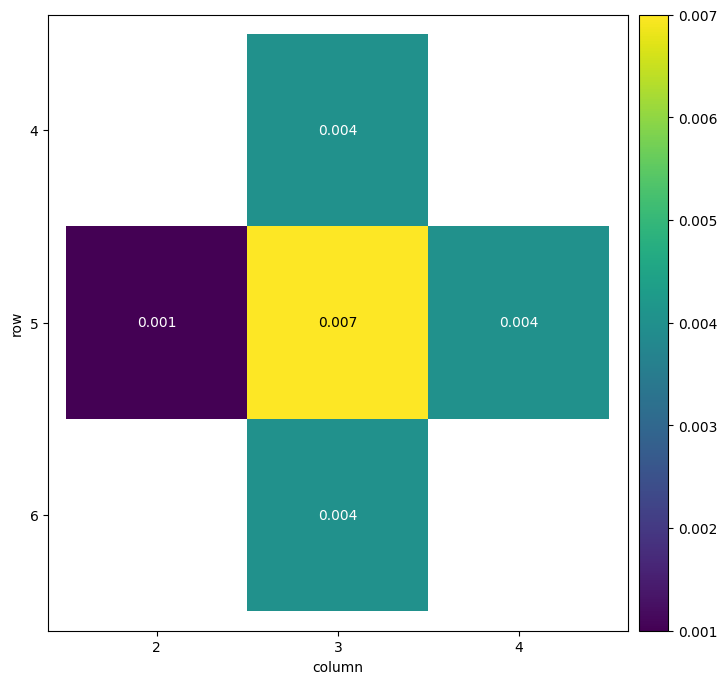
As a final exercise on this circuit, it's possible to display a 2D heatmap of measurement results. This will show which qubits measured a \(|1\rangle\) most often; on a hardware device, this could be used to highlight the performance of specific qubits. See Heatmaps for more on visualizing error.
meas_map = {qubit_map[measure_qubit]: sum(results.measurements['meas']) / repetitions}
data_map = {
qubit_map[dq]: sum(results.measurements[str(dq)[-1]]) / repetitions for dq in data_qubits
}
heatmap = cirq.Heatmap({**meas_map, **data_map})
heatmap.plot();
Stabilizer measurements on a large grid
The next examples scale up the stabilizer grid to a 2x3 block of three Z stabilizers and three X stabilizers. Combining both stabilizer types allows many types of error to be detected and compensated for, although some ambiguity still remains. It also manually maps the circuit to the hardware qubits.
A real logical qubit would require many more stabilizers to be fault-tolerant; however, this toy example is already near the upper bound of what a full statevector simulator can simulate on personal-level computers.
# Consider the following grid, where numbers represent
# measure qubits and letters represent data qubits:
#
# A
# B0C
# D1E2F
# G3H4J
# K5L
# M
#
# Center Z-plaquettes on [0, 3, 4] and
# X-plaquettes on [1, 2, 5]
# Instantiate the alphabetical data qubits and numerical measurement qubits.
grid_data_qubits = {x: cirq.NamedQubit(x) for x in 'ABCDEFGHJKLM'}
grid_meas_qubits = {x: cirq.NamedQubit(str(x)) for x in range(6)}
# Build the diamond shaped stabilizer circuit from six layered smaller stabilizers.
stabilizer_grid_circuit = cirq.Circuit(
cirq.H.on_each(grid_meas_qubits[x] for x in [1, 2, 5]),
*[cirq.CX(grid_data_qubits[x], grid_meas_qubits[0]) for x in 'ABCE'],
*[cirq.CX(grid_meas_qubits[1], grid_data_qubits[x]) for x in 'BDEG'],
*[cirq.CX(grid_meas_qubits[2], grid_data_qubits[x]) for x in 'CEFH'],
*[cirq.CX(grid_data_qubits[x], grid_meas_qubits[3]) for x in 'EGHK'],
*[cirq.CX(grid_data_qubits[x], grid_meas_qubits[4]) for x in 'FHJL'],
*[cirq.CX(grid_meas_qubits[5], grid_data_qubits[x]) for x in 'HKLM'],
cirq.H.on_each(grid_meas_qubits[x] for x in [1, 2, 5]),
*[cirq.measure(mq) for mq in grid_meas_qubits.values()],
*[cirq.measure(dq) for dq in grid_data_qubits.values()],
)
# Map the named qubits of the stabilizer circuit to GridQubits on the hardware.
qubit_map = {
cirq.NamedQubit('A'): cirq.GridQubit(4, 3),
cirq.NamedQubit('B'): cirq.GridQubit(5, 2),
cirq.NamedQubit('0'): cirq.GridQubit(5, 3),
cirq.NamedQubit('C'): cirq.GridQubit(5, 4),
cirq.NamedQubit('D'): cirq.GridQubit(6, 1),
cirq.NamedQubit('1'): cirq.GridQubit(6, 2),
cirq.NamedQubit('E'): cirq.GridQubit(6, 3),
cirq.NamedQubit('2'): cirq.GridQubit(6, 4),
cirq.NamedQubit('F'): cirq.GridQubit(6, 5),
cirq.NamedQubit('G'): cirq.GridQubit(7, 2),
cirq.NamedQubit('3'): cirq.GridQubit(7, 3),
cirq.NamedQubit('H'): cirq.GridQubit(7, 4),
cirq.NamedQubit('4'): cirq.GridQubit(7, 5),
cirq.NamedQubit('J'): cirq.GridQubit(7, 6),
cirq.NamedQubit('K'): cirq.GridQubit(8, 3),
cirq.NamedQubit('5'): cirq.GridQubit(8, 4),
cirq.NamedQubit('L'): cirq.GridQubit(8, 5),
cirq.NamedQubit('M'): cirq.GridQubit(9, 4),
}
stabilizer_grid_circuit = stabilizer_grid_circuit.transform_qubits(lambda q: qubit_map[q])
print(stabilizer_grid_circuit)
┌──┐ ┌────────┐ ┌──┐ ┌──┐ ┌────────┐ ┌───────┐ ┌───────┐ ┌────────────┐ ┌───────┐
(4, 3): ───@───M('A')────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│
(5, 2): ───┼───@──────────X─────M('B')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(5, 3): ───X───X─────────X┼─────X───────────M('0')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
││ │
(5, 4): ─────────────────@┼─────┼──────X────M('C')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(6, 1): ──────────────────┼─────┼─────X┼────M('D')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ ││
(6, 2): ───H──────────────@─────┼─────@┼────@─────────@──────H──────M('1')───────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(6, 3): ────────────────────────@──────┼────X─────────┼X──────@─────M('E')───────────────────────────────────────────────────────────────────────────────────────────────
│ ││ │
(6, 4): ───H───────────────────────────@──────────────┼@─────@┼─────@───────────H─────────M('2')─────────────────────────────────────────────────────────────────────────
│ ││ │
(6, 5): ──────────────────────────────────────────────┼──────X┼─────┼──────@────M('F')───────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(7, 2): ──────────────────────────────────────────────X───────┼─────┼─────@┼────M('G')───────────────────────────────────────────────────────────────────────────────────
│ │ ││
(7, 3): ──────────────────────────────────────────────────────X─────┼─────X┼────X─────────X───────────M('3')─────────────────────────────────────────────────────────────
│ │ │ │
(7, 4): ────────────────────────────────────────────────────────────X──────┼────@─────────┼─────@───────────X─────M('H')─────────────────────────────────────────────────
│ │ │ │
(7, 5): ───────────────────────────────────────────────────────────────────X──────────────┼─────X─────X─────┼─────X───────────────M('4')─────────────────────────────────
│ │ │ │
(7, 6): ──────────────────────────────────────────────────────────────────────────────────┼───────────@─────┼─────┼─────M('J')───────────────────────────────────────────
│ │ │
(8, 3): ──────────────────────────────────────────────────────────────────────────────────@─────────────────┼─────┼─────X─────────M('K')─────────────────────────────────
│ │ │
(8, 4): ───H────────────────────────────────────────────────────────────────────────────────────────────────@─────┼─────@─────────@─────────@──────────H────────M('5')───
│ │ │
(8, 5): ──────────────────────────────────────────────────────────────────────────────────────────────────────────@───────────────X─────────┼M('L')──────────────────────
│
(9, 4): ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────X──────────M('M')────────────
└──┘ └────────┘ └──┘ └──┘ └────────┘ └───────┘ └───────┘ └────────────┘ └───────┘
[Optional] View 3D circuit
Large circuits that are mapped to grids are suitable to be visualized in 3D with cirq_web, if you find it useful, as follows:
!pip install --quiet cirq-web
import cirq_web
circuit_vis = cirq_web.Circuit3D(stabilizer_grid_circuit)
display(circuit_vis)
Without noise
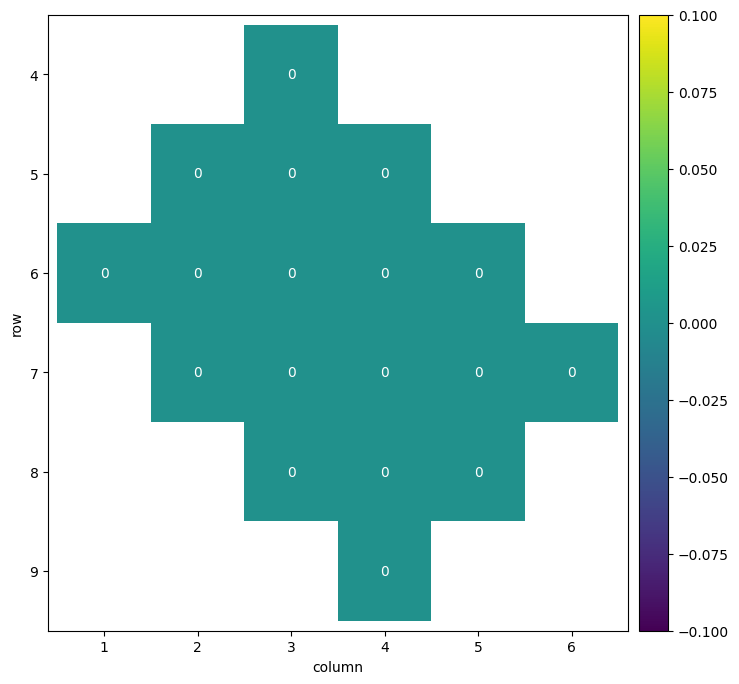
The noiseless version of the larger grid is slightly more exciting than the small grid example: the X measure qubits will measure a random state since their neighbors are initialized in the Z basis. However, subsequent measurements will remain consistent.
The example below runs a single cycle of the 2x3 grid 100 times, then does a Z-basis measurement of all data qubits. Since each of these is a separate execution of the circuit, no correlation is expected between repetitions.
noiseless_sim = qsimcirq.QSimSimulator()
repetitions = 100
start = time.time()
results = noiseless_sim.run(stabilizer_grid_circuit, repetitions=repetitions)
elapsed = time.time() - start
print(f'{repetitions} repetitions completed in {elapsed:.03f}s')
100 repetitions completed in 0.010s
# Set to view results from each repetition.
repetition = 0 # @param {type:"number"}
meas_map = {
qubit_map[q]: results.measurements[str(q)][repetition] for q in grid_meas_qubits.values()
}
data_map = {
qubit_map[q]: results.measurements[str(q)][repetition] for q in grid_data_qubits.values()
}
heatmap = cirq.Heatmap({**meas_map, **data_map})
heatmap.plot();
With hardware noise on the QVM
Adding in hardware-like noise means that subsequent cycles of a stabilizer might disagree with one another. These inconsistencies can be interpreted as various error modes, which can be decoded to compensate for the errors observed.
Decoding stabilizer error is a complex topic not covered here, but the pre-decoding results and data qubit measurements shown below may shed some light on how to approach this process.
test_stabilizer_grid_circuit = cirq.optimize_for_target_gateset(
cirq.Circuit(cirq.decompose(stabilizer_grid_circuit)),
context=cirq.TransformerContext(deep=True),
gateset=target_gateset,
)
print(test_stabilizer_grid_circuit)
┌──┐ ┌───────┐
(4, 3): ────────────────────────────@───M('A')─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│
(5, 2): ────────────────────────────┼────────────@───PhXZ(a=0.5,x=-0.5,z=0)────@───PhXZ(a=0.5,x=0.5,z=0)──────────────────────────────────────────────────────────────────────────────M('B')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(5, 3): ───PhXZ(a=0.5,x=-0.5,z=0)───@────────────@─────────────────────────────┼───────────────────────────@────────────────────────PhXZ(a=0.5,x=0.5,z=0)────PhXZ(a=0.5,x=-0.5,z=0)────────────────────────────────────────────────────────────────────────────────────@───PhXZ(a=0.5,x=0.5,z=0)─────────────M('0')────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(5, 4): ───────────────────────────────────────────────────────────────────────┼───────────────────────────@────────────────────────PhXZ(a=0.5,x=-0.5,z=0)─────────────────────────────────────────────────────────────────────────────────@───PhXZ(a=0.5,x=0.5,z=0)───┼────────────────────────────M('C')─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(6, 1): ───────────────────────────────────────────────────────────────────────┼───────────────────────────PhXZ(a=0.5,x=-0.5,z=0)───@────────────────────────PhXZ(a=0.5,x=0.5,z=0)─────────────M('D')──────────────────────────────────────┼───────────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(6, 2): ─────────────────────────────────────────────PhXZ(a=-0.5,x=0.5,z=-1)───@────────────────────────────────────────────────────@──────────────────────────────────────────────────────────────────────────────────────────────────────┼───────────────────────────┼─────────────────────────────────────@─────────────────────────────────@───PhXZ(a=-0.5,x=0.5,z=-1)───────────────────────────────M('1')────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(6, 3): ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼───────────────────────────@───PhXZ(a=0.5,x=-0.5,z=0)────────────@─────────────────────────────────┼─────────────────────────────@───PhXZ(a=0.5,x=0.5,z=0)───────────────────────────────────────────────────────────@──────────────────────────────M('E')─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(6, 4): ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=0.5,z=0)───PhXZ(a=0,x=1,z=0)───@───────────────────────────────────────────────────────────────────────────────────────────────────┼─────────────────────────────@────────────────────────────────────────────────────@─────────────────────────────@┼────PhXZ(a=-0.5,x=0.5,z=-1)─────────────────────────────────────────M('2')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ ││
(6, 5): ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼─────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)───@───PhXZ(a=0.5,x=0.5,z=0)─────┼┼───────────────────────────────────────────────────────@───M('F')────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ ││ │
(7, 2): ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)───@───PhXZ(a=0.5,x=0.5,z=0)────────────────────────────────────────────────────────────────────────────────────────┼┼───────────────────────────────────────────────────────┼────────────@────────M('G')──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
││ │ │
(7, 3): ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)────┼@───────────────────────────────────────────────────────┼────────────@─────────────────@────────────────────────────────@───────────────────────PhXZ(a=0.5,x=0.5,z=0)────────────────────────────────────M('3')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(7, 4): ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)────@─────PhXZ(a=0.5,x=0.5,z=0)──────────────────────────────┼──────────────────────────────@───@───PhXZ(a=0.5,x=-0.5,z=0)───┼────────────────────────────────────────────────@───PhXZ(a=0.5,x=0.5,z=0)───────M('H')───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(7, 5): ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)───@──────────────────────────────────@────────────────────────────┼────────────────────────────────────────────────┼───────────────────────────@───────────────────────────────────────────@────PhXZ(a=0.5,x=0.5,z=0)────M('4')─────────────────────────────────────────────────────────────────────────────────────
│ │ │ │
(7, 6): ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────────────────────────────────────────┼───────────────────────────@───M('J')──────────────────────────────────┼────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(8, 3): ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────@───────────────────────PhXZ(a=0.5,x=-0.5,z=0)───┼───────────────────────────────@────────PhXZ(a=0.5,x=0.5,z=0)────M('K')┼────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
│ │ │
(8, 4): ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=0.5,z=0)───PhXZ(a=0,x=1,z=0)────────@───────────────────────────────@───────────────────────────────────────┼─────────────────────────────@─────────────────────────────────@───PhXZ(a=-0.5,x=0.5,z=-1)─────────────────────M('5')───
│ │ │
(8, 5): ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────@────PhXZ(a=0.5,x=-0.5,z=0)───@────────PhXZ(a=0.5,x=0.5,z=0)────┼─────────────────────────────M('L')─────────────────────
│
(9, 4): ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────PhXZ(a=0.5,x=-0.5,z=0)───@───PhXZ(a=0.5,x=0.5,z=0)──────────────M('M')────────────
└──┘ └───────┘
repetitions = 100
start = time.time()
results = sim_engine.get_sampler(processor_id).run(
test_stabilizer_grid_circuit, repetitions=repetitions
)
elapsed = time.time() - start
print(f'{repetitions} repetitions completed in {elapsed:.03f}s')
100 repetitions completed in 5.278s
# Set to view results from each repetition.
repetition = 0 # @param {type:"number"}
meas_map = {
qubit_map[q]: results.measurements[str(q)][repetition] for q in grid_meas_qubits.values()
}
data_map = {
qubit_map[q]: results.measurements[str(q)][repetition] for q in grid_data_qubits.values()
}
heatmap = cirq.Heatmap({**meas_map, **data_map})
heatmap.plot();